AWG（任意波形發生器）復數模式和實數模式的區別

　   事實上，復數模式和實數模式最大的區別在于：數字可控振蕩器(NCO)和實時的計算過程。我們需要明確的是，無論是實數還是復數模式，DG70000的最大存儲深度是1.5Gpts，數據帶寬也是有限的。這些因素限制了實數模式的靈活性和信息載量。以下用兩個例子說明它們之間的區別：

　　例1特性對比

　　1.5Gpts的實數波表，DG70000最多可以以10GSa/s的DAC速率輸出。由于兩倍內插的存在，波表的有效輸出速率是5GSa/s。所以該波表的持續時間是0.3秒，覆蓋了DC-2GHz的模擬帶寬(第一奈奎斯特區域，Fs/2.5=2GHz，以下相同)。

　　當然用戶也可以犧牲帶寬來換取更高的持續時間，調小輸出速率即可。而1.5Gpts的復數波表，分為兩個750Mpts的實數波表，DG70000最多可以以12GSa/s的DAC速率輸出。此時，波表的有效輸出速率為3GSa/s，持續時間為0.5s。基帶帶寬為DC-1.2GHz。通過NCO搬移后最高輸出頻率可以達到5GHz。

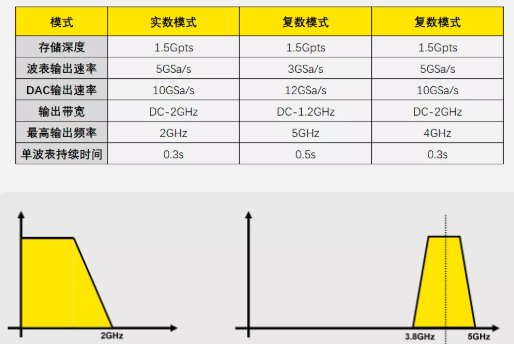
　　圖4 最大輸出頻率下的實數和復數模式頻率范圍

　　可以發現是的，實數和復數模式的輸出速率雖然近似，但是由于NCO的存在，最高輸出頻率和輸出持續時間都優于實數模式。在頻域信號方面，復數模式更占優勢。而在復雜的寬帶時域信號方面，實數模式更占優勢，一個波表即涵蓋了所有的內容，而不需要進行各種計算。

　　例2 波表截斷

　　如果令IQ基帶信號為一對正交的正弦波，代入i(t)和q(t)并進行化簡，可以發現基帶信號被NCO整體上變頻，并且最終輸出為一個正弦單音信號。讓我們以輸出一個正弦信號為例，來直觀感受復數模式下NCO和實時計算帶來的一些特性區別。

　　我們知道，任意波形發生器的最終輸出取決于波表的內容和輸出采樣率。如果想要獲得良好的輸出質量(正弦波)，應該如圖5中所示的樣子，沒有離散和突變的點出現。

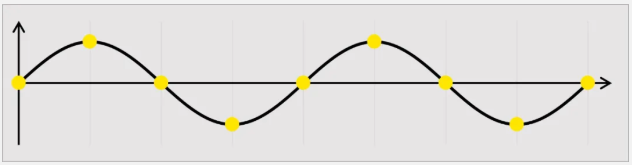
　　圖5 使用整倍數生成實數波表輸出

　　一般來說，實數模式下都可以通過調節波表輸出速率為目標頻率的整倍數(或有限小數倍數)來解決。如果每周期點數是無限小數，那么永遠無法達到首尾良好銜接，就會出現波表截斷。

　　圖5中展示了一個周期是4個點的情況，圖6中展示了一個周期是5.70125…個點這種狀況。如果此時建立一個有6個點的波表，那當DG70000循環輸出波表到第7個點(黃色圓點)的時候，就會偏離原本的數值，引入相位抖動噪聲(截斷)。而使用復數模式的時候，所有的點(橙色方塊)都是通過基帶和NCO數據實時計算得到的，其長度無窮無盡且精準，就避免了這種狀況的發生。當然，前提是復數基帶波表是波表輸出速率的整倍數。

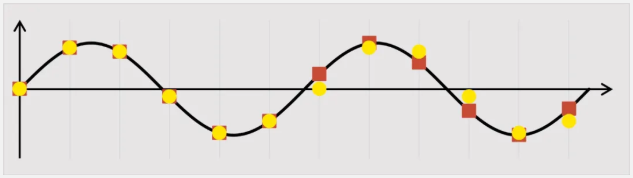
　　圖6 使用小數倍數生成實數波表輸出和復數模式輸出

　　以下的例子展示了如何通過復數模式實現無雜散小數倍頻率輸出。在一些特殊應用場景下，需要給被測儀器同時提供100MHz和990MHz的正弦信號，然而這兩個信號是無法獲得一個共同的整倍數采樣率的。這意味這如果都采用實數模式輸出，其中某一個信號一定會帶有截斷噪聲。

　　這時候，就可以將DG70000的一個通道配置在復數模式，另一個通道配置在實數模式，輸出速率設置在5GSa/s。采用內置插件編譯1MHz的基帶信號，然后設置NCO為989MHz將1MHz的基帶正弦信號搬移到990MHz。另一個通道可以直接用實數模式輸出100MHz的信號。此時可以同時在兩個通道輸出高質量的無截斷噪聲的正弦信號。

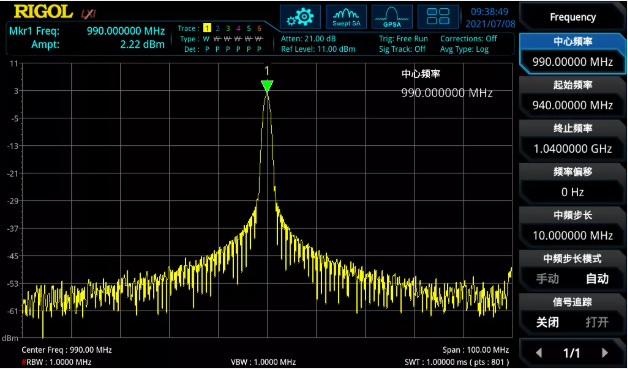
　　圖7 攜帶了雜散的990MHz正弦信號(實數模式)，5GSa/s　　

　　圖8 優化了雜散的990MHz正弦信號(復數模式)，5GSa/s