什么是傅里葉變換？傅里葉變換怎么疊加？

傅里葉變換是一種在數學和工程領域廣泛應用的工具，它允許我們將一個復雜的信號分解成簡單的正弦波和余弦波的疊加。這種變換以法國數學家約瑟夫·傅里葉命名，他在19世紀早期對熱傳導的研究中發現了這種變換。

傅里葉變換的基本思想是，任何一個周期信號都可以看作是無限多個不同頻率的正弦波和余弦波的疊加。這些正弦波和余弦波的頻率可以是連續的，也可以是離散的。對于離散的情況，這些正弦波和余弦波被稱為離散傅里葉變換（DFT）；對于連續的情況，它們被稱為連續傅里葉變換（CT）。

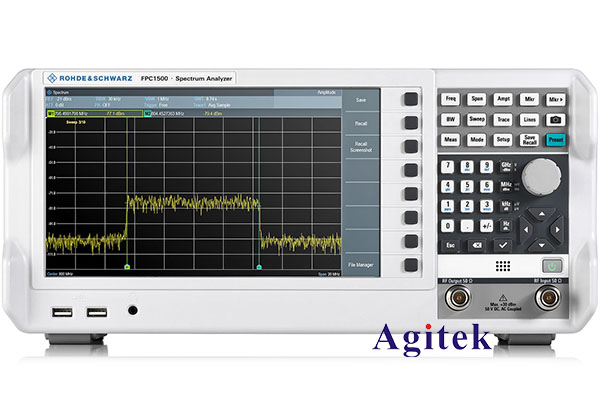
傅里葉變換的公式如下：

X(ω) = ∫x(t)e^(-iωt) dt

其中，X(ω)表示頻率域中的信號，x(t)表示時域中的信號，ω表示角頻率，i表示虛數單位。

傅里葉變換的疊加原理表明，如果兩個信號x1(t)和x2(t)的頻率分量是相互獨立的，那么它們的傅里葉變換也是相互獨立的。這意味著，如果我們有兩個信號x1(t)和x2(t)，那么它們的傅里葉變換可以分別進行，然后再將得到的頻率域信號進行疊加。

疊加原理在信號處理中有很多應用。例如，在音頻合成中，我們可以通過將多個不同頻率的正弦波疊加來創建一個復雜的音頻信號。在圖像處理中，我們可以通過將多個不同頻率的分量疊加來對圖像進行濾波或增強。